Youguang Chen

Youguang Chen

Ph.D. student, Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin

SUBSET SELECTION FOR COLD STARTING SEMI-SUPERVISED LEARNING

Problem description

Semi-supervised learning (SSL) seeks to largely alleviate the need for labeled data by allowing a model to leverage unlabeled data. We are considering the problem of selecting training points to label for a SSL classification task, especially in the regime where the number of labeled points is a small multiple of the number of classes $C$, say $2C$ or $4C$. We deploy the features from the stae-of-the-art self-supervised learning model SimCLR. We evaluate the quality of the selected samples by using the SSL model FixMatch.

Results

  • We propose a new sampling method. Suppose our sampling budge is $k$. First, we randomy select a subset using importance sampling where the probability of choosing a point is proportional to it’s spectral leverage score. Then we us K-means to divid the subselected samples into $k$ parts and select the $k$ points nearest to the cluster centers.
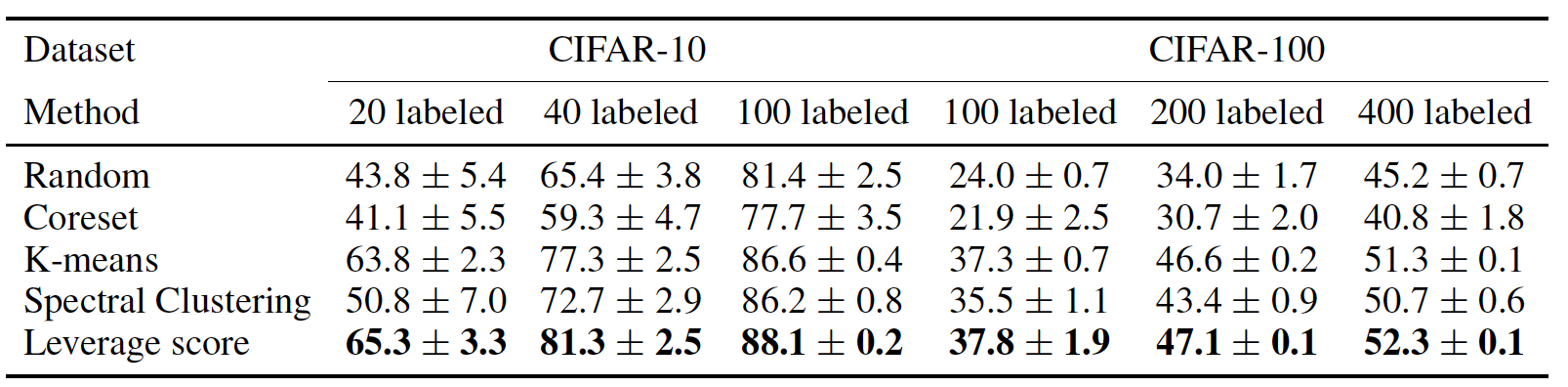
  • We show our sampling method outperform than many other methods: random, coreset, K-means, spectral clustering, and maximum mean discrepancy (MMD). The comparison of different sampling methods on CIFAR-10 with 20 labeling budget is shown in the above image. We also compare different methods by training the logistic regression model with only the labeled samples (accuracy on test data of CIFAR-10 and CIFAR-100 with different labeling budges are shown in the above table). We also conduct logistic regression on ImageNet with 2000 labeled samples. Our method outperforms than other methods.



KNN-DBSCAN: A DBSCAN IN HIGH DIMENSIONS

Paper and Code

Problem description

DBSCAN is a broadly used density-based clustering algorithm. It requires two user-defined density parameters: radius of a neighborhood $\epsilon$ and neighborhood size of core points $k$. DBSCAN constructs undirected $\epsilon$-nearest neighbor graph ($\epsilon$-NNG) in its implementation. However, constructing the graph in high dimensions is expensive and its structure becomes more sensitive to $\epsilon$ with increasing dimension. Furthermore, the existing parallel implementations of DBSCAN do not consider the challenges with high-dimensional datasets.

Results

KNN-DBSCAN

  • We propose a new density-based clustering algorithm KNN-DBSCAN to enable the using of directed $k$-nearest neighbor graph ($k$-NNG). One benefit of using $k$-NNG it that there exist effective approximate randomized algorithms for $k$-NNG computation. In addition, the memory requirements for $k$-NNG always remain $O(nk)$, whereas for $\epsilon$-NNG can explode to $O(n^2)$ (n is the number of points).
  • We perform theoretical analysis to discuss the relation of KNN-DBSCAN to the original DBSCAN. We also empirically show that both of the two methods have similar clustering performances given same input parameters ($\epsilon$ and $k$).

Parallel Algorithms

  • We design and implement a hybrid MPI/OpenMP parallel algorithm of our method. We propose an approximate minimum spanning tree (MST) algorithm to accommodate the distributed setting, and prove that the approximate algorithm has the same clustering results as the exact MST.
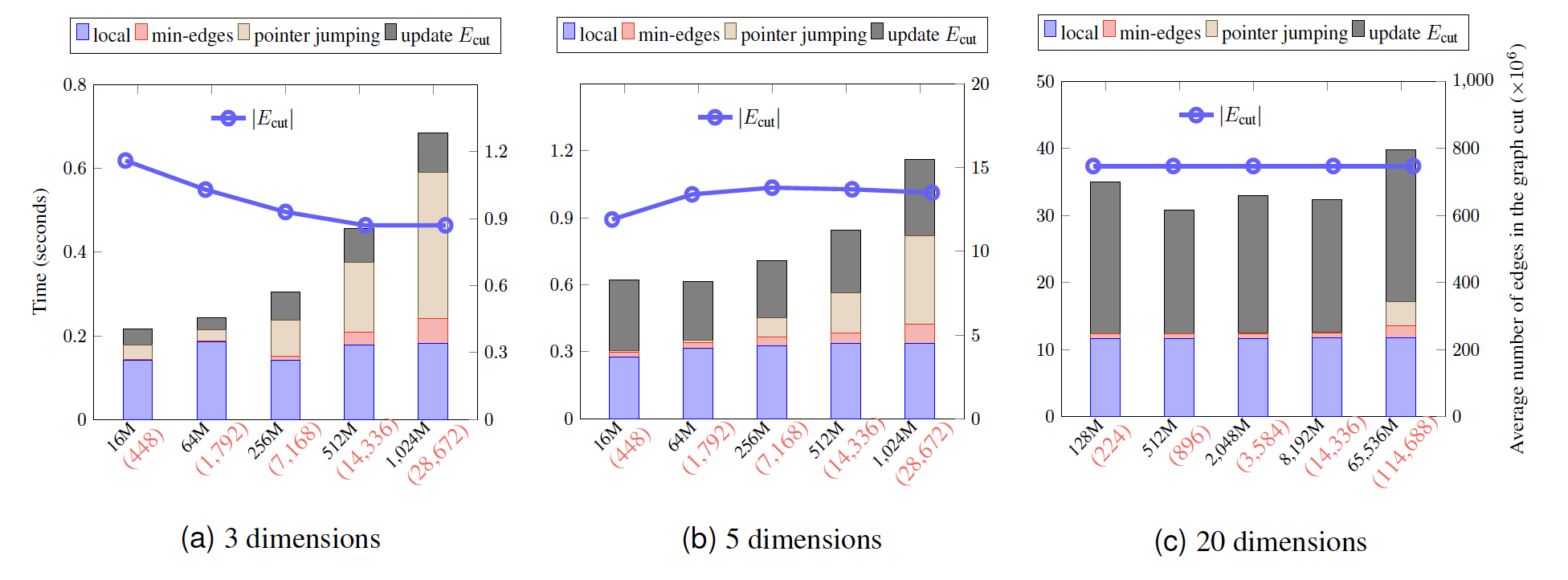
  • We perform weak and strong scaling tests on synthetic datasets up to 32 dimensions. In our largest run, we clustered 65 billion points in 20 dimensions in less than 40 seconds using 114,688 x86 cores (weak scaling results are the figure shown above).
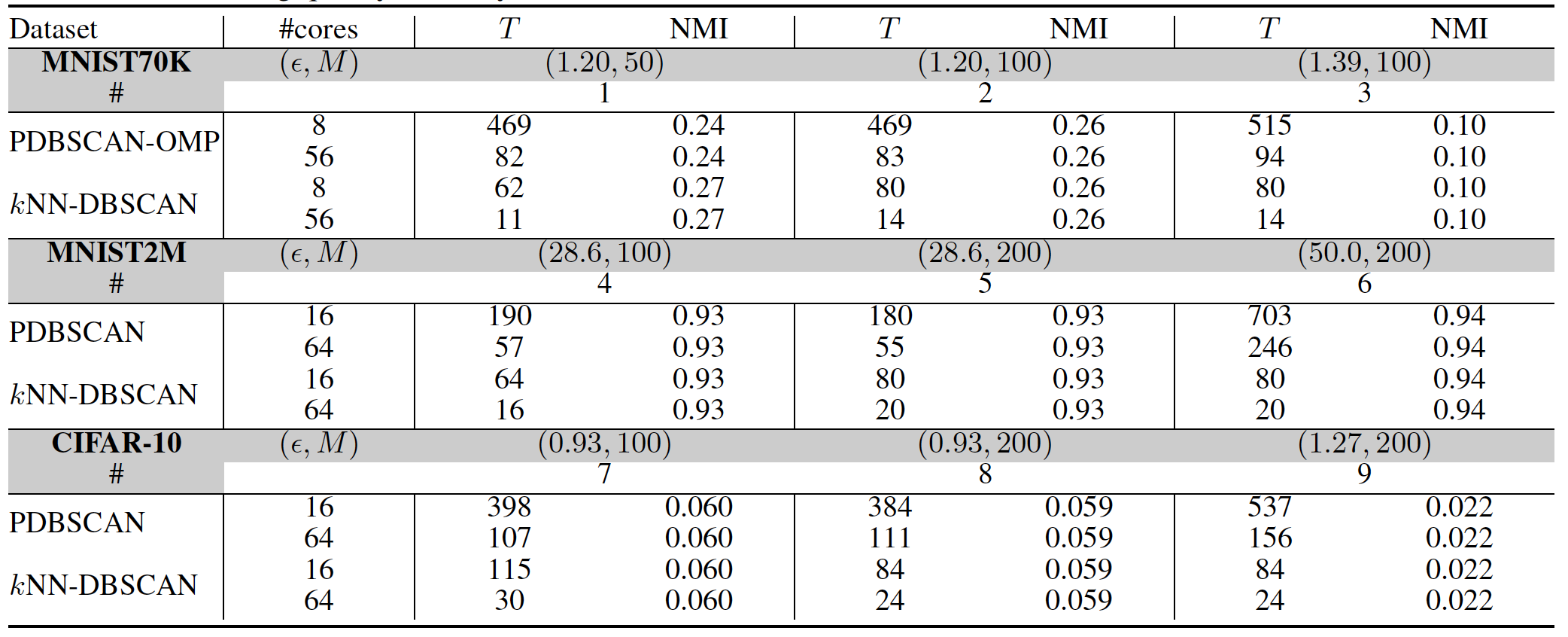
  • We compare our method with a state-of-the-art parallel DBSCAN code PDBSCAN (the table shown above). Our implementation is about 3$\times$-37$\times$ faster, depending on the dataset; and we construct a simple dataset where the $\epsilon$-range search in PDBSCAN can easily fail.



A GALERKIN METHOD FOR MODELING FLOW IN POROUS MEDIA WITH IMMERSED FAULTS

Paper

Problem description

Modling flows in porous media with immersed faults (material discontinuities) is challenging because the exact pressure along the fault $p \in L^2(\Omega)$ is discontinuous and the velocity is coupled with the pressure in the partia differential equations. Although the mixed finite element method (FEM) is a traditional approach to solve this problem, it results in unsymmetric and badly conditioned linear systems. Our goal is to derive and solve approximating PDEs using Galerkin method.

Results

Methodology

  • We derive new approximate PDEs with pressure solutions in $H^1$ Sobolev space, i.e. $p_\epsilon \in H^1(\Omega)$. We prove that the approximation is well-defined in $L^2$-sense, i.e. approximated pressure solutions converge to the exact pressure: $p_\epsilon \xrightarrow{L^2(\Omega)} p$ as $\epsilon \xrightarrow{} 0^+$.
  • When $d=1$ ($d$ is the domain dimension), we decouple pressure and velocity in the PDEs exactly. When $d\geq 2$, we decopule pressure and velocity approximately using Taylor expansions. The new PDEs related to the approximated pressure can be easily solved by the continuous Galerkin formulation and results in better-conditioned symmetric positive definite linear system that can be optimally solved using multigrid.

Numerical Experiments

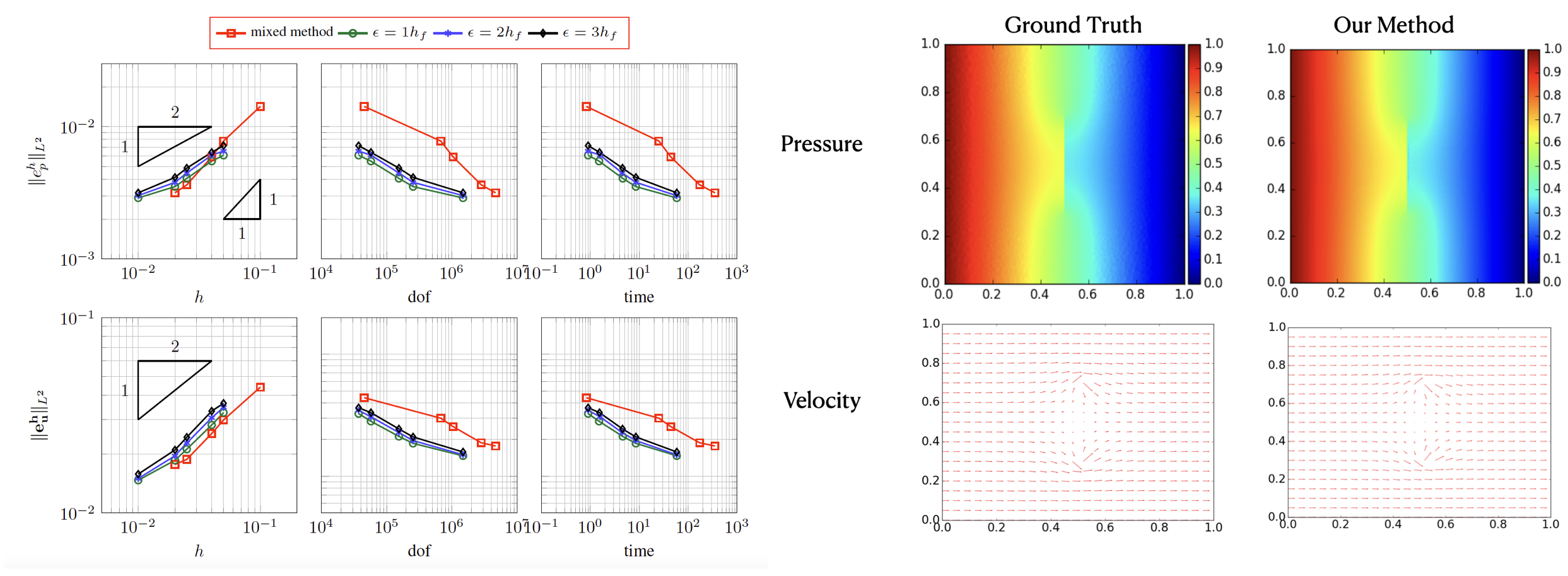
  • We implement the new method and test preconditioned iterative Krylov solves. To evaluate the performance of the new scheme, we develope analytical models to carefully tune model parameters and tested them in practice.
  • Our experiment results show that the velocity convergence rate is almost $O(h^\frac{1}{2})$ (h is the mesh size). In one of our 3D tests, the new method is about 7$\times$ -30$\times$ faster than the mixed FEM at given pressure error, or 3$\times$-17$\times$ faster at given velocity error.